TLS/암호 알고리즘 쉽게 이해하기(10) - Hash
Hash 함수란 임의의 길이의 데이타를 축약하여 고정된 길이의 데이타로 매핑하는 함수를 말한다.
데이타 검색을 위한 hash 함수, 데이타 손상을 검출하기 위한 CRC32 도 hash 함수 이지만, 이 글에서 언급하는 것은 암호화 해시 함수이다.
각 용도에 따라서 해시 함수의 특성은 다음처럼 다를 수 있다.
- 데이터 검색용: 모든 입력 데이타에 대해서 hash 결과값이 균등 분포를 가져야 한다.
- 데이타 손상 검출용: 원하는 비트 개수 까지의 오류에 대해서 정확히 검출되어야 하고, 알고리즘에 따라서 제한된 비트 개수 까지 오류 복원이 가능하여야 한다.
- 암호화용: 해시 값으로 원본을 추측 불가능하여야 하고, 임의의 두 데이타가 동일한 해시값을 가지는 충돌이 실제적으로 불가능하여야 한다.
암호화 hash의 특징
우선 용어를 정리해 보자.
- 역상(pre-image): hash 전의 데이타 원본
- 저항성(resistance): 내성
- 충돌(collision): 임의의 데이타의 hash 결과값이 동일한 값을 가지는 것
암호화 hash 함수는 다음 조건을 만족하여야 한다.
- 제 1 역상 저항성(first pre-image resistance): 해시 값으로 원본 메시지를 찾는 것이 현실적으로 불가능
- 제 2 역상 저항성(second pre-image resistance): 동일한 해시 값을 가진 2개의 데이타를 찾는 것(충돌)이 현실적으로 불가능
제1역상 저항성을 만족하기 위하여는 원본 데이타의 1bit가 변경되면 결과값이 무작위한 난수처럼 변경되어야 한다. 이를 만족하고, hash 함수가 128bit의 결과값을 가진다면, $2^{128}$ 번 이상의 시도를 하여야 충돌을 찾을 수 있다.
하지만, 제 2 역상 저항성, 즉, 임의의 2개 메시지가 동일한 값을 가지는 것은 위의 것보다는 더 쉽게 찾을 수 있다.
이를 Birthday Paradox 라고 하는데, 간단하게 설명하면 다음과 같다.
- 나와 같은 생일을 가진 사람을 찾으려면 확률적으로 몇 명을 찾아보아야 할까?
- 365명 이상
위의 질문은 쉽게 이해가 갈것이다.
그런데, 다음 질문의 답은 얼마가 될까?
- 같은 생일을 가진 사람이 있을 확률이 50% 이상이려면 얼마의 사람을 모아야 할까?
답은 23명이다. 즉, 한 방안에 23명이 모여 있다면 확률적으로 같은 생일을 가진 사람이 있을 확률이 1/2 이상이라는 말이다.
이것이 제 2 역상 저항성 충돌 문제로, 하나의 원본과 동일한 해시 값을 가진 다른 메시지를 만들어 내는 것은 어렵지만, 동일한 해시 값을 가진 두 메시지를 만들어 내는 것은 상대적으로 쉽다는 것이다.
수학적으로 보면 총 경우의 수를 N, 선정한 임의의 개수를 r이라고 하면 충돌이 발생할 가능성은 다음과 같다.
$$ \Pr \approx 1 - e^{\frac{-r^2}{2N}} $$
간단히 말하면 $n$ bit의 결과값을 hash 함수에 대해서 단순하게 찾는다면 제1역상은 $2^n$ 회의 연산이 필요하지만, 제2역상은 $2^{n/2}$ 회의 연산이면 된다.
좀더 직관적으로 보기 위해 32bit의 hash 함수를 보면 단순 무식 충돌 찾기의 횟수는 다음과 같다.
- 제1역상 찾기: $2^{32} = 4,294,967,296$
- 제2역상 찾기: $2^{32/2} = 65,536$
제1역상은 42억번의 시도를 해보아야 하지만 제2역상은 6만번이면 찾을 수 있다.
다만 이렇게 찾으려면 65,536개의 결과값을 저장하고 비교해야 하는데, 비트수가 커지면 결과를 저장할 공간이 무한히 커져야 하는 문제가 있다. 물론 메모리를 적게 사용하는 위한 Pollard’s rho algorithm와 같은 공격 방법들이 있다.
Hash 함수의 구성
현재 사용하는 MD5, SHA-1, SHA-2 방식은 전체 메시지를 압축하여 하나의 결과값을 만드는 구조가 아니라, AES 블럭 암호화 처럼 블럭단위로 압축을 하고, 이를 연쇄적으로 이어가는 방식이다.
Hash에서 이 구조를 Merkle–Damgård construction 라고 하고, 위키피디아에 있는 아래 그림과 같은 구조이다.
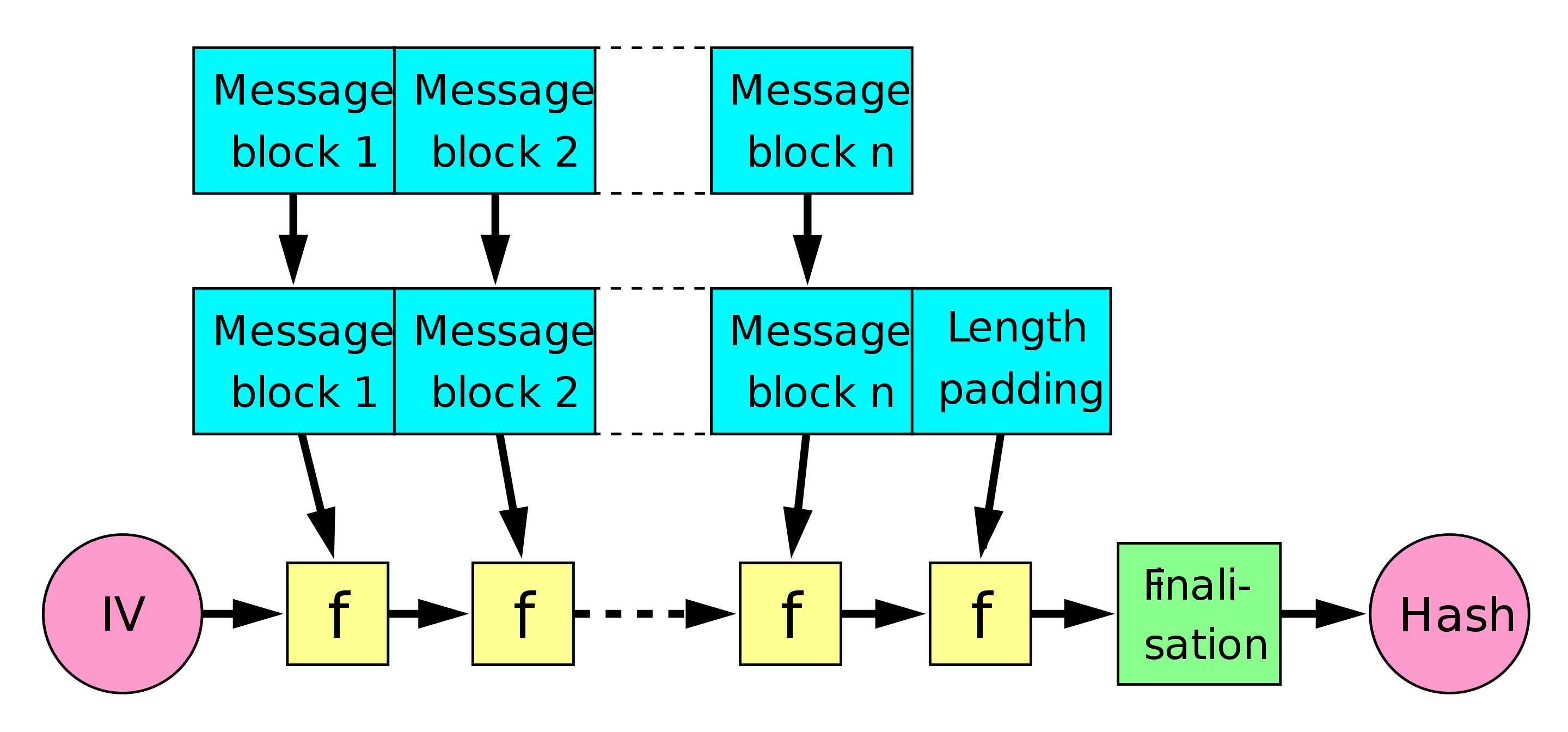
PKCS#1 v1.5 padding
이전 글의 Block Cipher Mode의 AES-CBC 모드처럼 구성된 것이라고 보면 된다.
실제로 Davies-Meyer 방식의 경우 암호함수를 이용하여 hash를 구성하기도 한다.
이와 같은 체인 구조의 경우 안전한 함수를 사용한 경우 어떠 크기의 데이타라도 압축하여 hash 값을 만들 수 있으나, 취약점이 발견된다면 데이타를 조작 가능한 문제점을 가지고 있다.
Hash 함수들
가장 많이 사용하는 hash 함수는 MD5 와 SHA 계열이다.
MD5는 1992년 RFC 1321로 정의된 것이고, SHA(Secure Hash Algorithm)는 미국 NIST에서 제정한 표준이다. SHA는 버전에 따라서, SHA-1, SHA-2, SHA-3 로 구분이 된다. SHA-2, SHA-3는 몇가지의 hash 값 길이를 제공한다.
보통 특정한 언급없이 SHA-256, SHA-384, SHA-512 와 같이 비트길이를 적은 것은 SHA-2 말하는 것이다. SHA-3 의 경우 SHA3-256 과 같이 표기한다.
각 함수들의 특징을 비교하면 다음과 같다.
| Algorithm | Name | Output Size(bit) | Internal Size(bit) | Block Size(bit) | 길이 한계 |
|---|---|---|---|---|---|
| MD5 | MD5 | 128 | 128 | 512 | $2^{64}-1$ |
| SHA-1 | SHA-1 | 160 | 160 | 512 | $2^{64}-1$ |
| SHA-2 | SHA-224 | 224 | 256 | 512 | $2^{64}-1$ |
| SHA-256 | 256 | 256 | 512 | $2^{64}-1$ | |
| SHA-384 | 384 | 512 | 1024 | $2^{128}-1$ | |
| SHA-512 | 512 | 512 | 1024 | $2^{128}-1$ | |
| SHA-3 | SHA3-224 | 224 | 1600 | 1152 | |
| SHA3-256 | 256 | 1600 | 1088 | ||
| SHA3-384 | 384 | 1600 | 832 | ||
| SHA3-512 | 512 | 1600 | 576 |
현시점에서 MD5, SHA-1은 충돌이 발견되어 더 이상 암호 용도로는 사용을 제한하고, TLS 1.2 부터는 제외되었다.
MD5, SHA-1, SHA-2 의 경우 기본 구성은 동일한 Merkle–Damgård construction 구조로, SHA-2 도 언젠가는 유사한 취약점이 발견될 수도 있다. 물론 현재까지는 SHA-2는 안전한 암호화 hash 함수이다.
SHA-1, SHA-2의 입력 데이타의 길이 제한이 있는 이유는 입력 데이타를 블럭 크기로 맞추면서 패딩 시 데이타 크기를 기록하기 때문에 이 부분으로 인하여 제한이다.
MD5, SHA-1 취약점
아래 링크를 보면 이와 같은 MD5 의 취약점을 이용하여 동일한 hash 값을 가지지만 다른 동작을 하는 프로그램을 직접 만들어 볼 수도 있다.
Merkle–Damgård construction 구조에서 각 블럭은 initial vertor(또는 이전 블럭의 결과값) 과 데이타 블럭이 압축 함수를 거치는 구조이다.
그런데 특정 블럭 $M, M’, N, N’$ 이 있는 경우 어떠한 initial vector $s$ 에 대해서도 다음과 같은 조건을 만족하는 경우가 발견되었다.
$$ f(f(s, M), M’) = f(f(s, N), N’) $$
이 의미는 데이타 블럭에 $M, M’$ 이 있는 경우 이를 $N, N’$ 으로 대치 하여도 동일한 해시값을 가진 경우가 생긴다. 이와 같은 방식으로 중간의 특정 블럭을 교체하여, 동일한 hash 값을 가지도록 하고, 이 블럭을 참조하여 다른 동작을 하는 프로그램을 만든다.
실행 파일도 그렇지만 인증서와 같은 문서도 이처럼 충돌되도록 만드는 것도 가능하다고 한다.
SHA-1 의 경우에도 마찬가지로 충돌 방법이 발견되었고 아래 링크에서 확인해 볼 수 있다.
SHA-3
MD5에서 나온 충돌 문제처럼, 임의의 문서에서 문서의 내용을 악의적으로 바꿀 수 있는 비트를 몇십개를 선정해서 이를 알고리즘의 취약점이나 brithday attack 과 같은 방법으로 찾아 나가면 유사한 체인 구조를 가진 SHA-2 도 취약점이 발견될 가능성이 있다.
이런 염려로 NIST에서는 2007년에 기존의 SHA-1, SHA-2 와는 구조와는 완전히 다른 해시 함수를 공모를 시작하여 최종적으로 2015년에 Keccak 해시 함수를 SHA-3 로 선정하여 2015년에 발표하였다.
이 방식의 특징은 위의 표에서 보듯이 내부 1600비트의 상태를 치환해서 SHA-2 와 동일한 결과 비트를 만들어 낸다. 십년 이상의 연구 결과로 나온 것으로 악용 가능한 취약점이 전혀 없는 강한 알고리즘이다.
하지만 아래와 같이 속도를 측정해보면 동일한 출력 비트에 비해서 SHA-1, SHA-2 에 비하여 상대적으로 느리다는 단점이 있다.
$ openssl speed -evp sha1
Doing sha1 for 3s on 16 size blocks: 12130080 sha1's in 3.00s
Doing sha1 for 3s on 64 size blocks: 9737560 sha1's in 2.99s
Doing sha1 for 3s on 256 size blocks: 6238334 sha1's in 3.00s
Doing sha1 for 3s on 1024 size blocks: 2627777 sha1's in 2.99s
Doing sha1 for 3s on 8192 size blocks: 407163 sha1's in 2.99s
Doing sha1 for 3s on 16384 size blocks: 207609 sha1's in 3.00s
OpenSSL 1.1.1m 14 Dec 2021
built on: Tue Dec 14 15:45:01 2021 UTC
options:bn(64,64) rc4(16x,int) des(int) aes(partial) idea(int) blowfish(ptr)
compiler: clang -fPIC -arch x86_64 -O3 -Wall -DL_ENDIAN -DOPENSSL_PIC -DOPENSSL_CPUID_OBJ -DOPENSSL_IA32_SSE2 -DOPENSSL_BN_ASM_MONT -DOPENSSL_BN_ASM_MONT5 -DOPENSSL_BN_ASM_GF2m -DSHA1_ASM -DSHA256_ASM -DSHA512_ASM -DKECCAK1600_ASM -DRC4_ASM -DMD5_ASM -DAESNI_ASM -DVPAES_ASM -DGHASH_ASM -DECP_NISTZ256_ASM -DX25519_ASM -DPOLY1305_ASM -D_REENTRANT -DNDEBUG
The 'numbers' are in 1000s of bytes per second processed.
type 16 bytes 64 bytes 256 bytes 1024 bytes 8192 bytes 16384 bytes
sha1 64693.76k 208429.38k 532337.83k 899947.71k 1115544.92k 1133821.95k
$ openssl speed -evp sha256
...
type 16 bytes 64 bytes 256 bytes 1024 bytes 8192 bytes 16384 bytes
sha256 50676.02k 141399.80k 316782.51k 462059.86k 532104.65k 531109.21k
$ openssl speed -evp sha3-256
...
type 16 bytes 64 bytes 256 bytes 1024 bytes 8192 bytes 16384 bytes
sha3-256 28803.58k 115073.18k 292266.75k 367422.16k 420298.92k 428512.60k결과를 정리해 보면 다음과 같다. 아래 결과는 해당 블럭을 암호화 했을 때 동일 시간에서 처리량이다.
| type | 16 bytes | 64 bytes | 256 bytes | 1024 bytes | 8192 bytes | 16384 bytes |
|---|---|---|---|---|---|---|
| sha1 | 64693.76k | 208429.38k | 532337.83k | 899947.71k | 1115544.92k | 1133821.95k |
| sha256 | 50676.02k | 141399.80k | 316782.51k | 462059.86k | 532104.65k | 531109.21k |
| sha3-256 | 28803.58k | 115073.18k | 292266.75k | 367422.16k | 420298.92k | 428512.60k |
SHA-1은 160bit 라 256bit인 SHA-2, SHA-3와는 직접 비교는 되지 않지만, 어쨋든 SHA-1 이 빠르기도 하고 사용하던 관성에 있어 아직도 많이 사용하고 있다.
예를 들어 git 은 현재도 default로 SHA-1 hash 를 이용하여 commit 버전 관리를 하고 있고, 2020년 10월 v2.29 부터 expreimental 기능으로 SHA256을 지원하기 시작한다.
SHA-3의 경우 SHA-2 와 비교하여 속도가 느리기도 하고, 아직까지는 SHA-2 취약점이 발견되지 않았기 때문에 한 동안은 SHA-2 가 더 많이 이용될 것으로 보인다.
Openssl에서는 openssl dgst 명령으로 hash 함수의 결과를 확인해 볼 수 있고 자주 사용하다 보니 별도의 명령으로도 나와 있다.
$ openssl dgst -sha256 mydata.txt
SHA256(mydata.txt)= 4795a1c2517089e4df569afd77c04e949139cf299c87f012b894fccf91df4594
$ openssl sha256 mydata.txt
SHA256(mydata.txt)= 4795a1c2517089e4df569afd77c04e949139cf299c87f012b894fccf91df4594마치며
보안이 강조되는 프로그램에서 hash를 사용하여야 한다면 현재로서는 SHA-256 이 가장 적절한 솔루션일 것이다.
혹시나 SHA-2 방식의 구조가 염려되나 SHA-3 느린 성능이 불만이라면, Blake2 hash 함수와 같은 것도 검토해 볼 수 있다.
암호화 라이브러리에 지원되는 hash 함수들은 아래 링크에서 찾아볼 수 있다.
다른 암호도 마찬가지이지만, 특별한 이유가 없다면 직접 구현하는 것 보다는 이와 같은 공개적으로 검증된 알고리즘과 암호화 라이브러리를 사용하는 것이 좋을 것이다. 직접 구현을 하다보면 사소한 실수로 암호 강도가 크게 떨어지는 문제가 발생할 수 있다.