TLS/암호 알고리즘 쉽게 이해하기(11) - Elliptic Curve Cryptography(ECC)
타원 곡선(Elliptic Curve)는 일반적으로 생각하는 가로 세로비가 다른 길쭉한 원을 말하는 것이 아니라 다음과 같은 공식으로 구성된 곡선을 말한다.
$$y^2 = x^3 + ax + b$$
$a$ 와 $b$ 는 임의의 수로 특이점이 없도록 다음과 같은 조건을 만족하여야 한다.
$$4 a^3 + 27b^2 \neq 0$$
이와 같은 조건을 만족하는 곡선은 다음과 같은 모양을 가진다.

b=1, a=2~-3 일 때의 모양
만일 위 조건을 만족하지 않는 경우는 아래와 같이 첨 점이거나 교차하는 특이점이 있다.
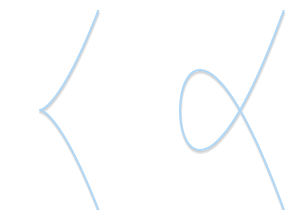
왼쪽: $y^2=x^3$, 오른쪽: $y^2=x^3-3x+2$
참고 자료
타원 곡선은 오래된 역사를 가진 것으로 그 역사와 이론적인 배경을 이해하는 것은 쉬운 일은 아니다.
그래서 이글에서도 타원곡선 암호의 특성을 이해하는데 필요한 부분만 정리하기로 한다.
이 글에서 참고한 링크는 다음과 같다.
- Elliptic Curve Cryptography - Andrea Corbellini: 타원곡선에 대하여 아주 아주 잘 정리된 시리즈의 글로, 여기에 정리한 내용은 이 글을 요약한 것이라고 할 수 있다. 아래 글을 한번 읽어 보는 것을 추천한다. 다음과 같은 시리즈로 되어 있다.
- Elliptic Curve Cryptography Explained – Fang-Pen’s coding note: 저자가 작성한 python notebook 예제를 직접 실행하면서 타원곡선 암호를 이해하기 좋다.
첫번째 링크에서 제공하는 Elliptic Curve Visual Tool을 이용하여 실수와 모듈러 정수군에서의 연산 결과를 직접 확인하면서 이해하는 것도 좋고, 두번째 링크에서 제공하는 Python 코드로 타원곡선 연산을 수행하는 과정을 직접 확인해 보는 것도 좋다. Python Jupyter Notebook은 Google Colab에서 GitHub link를 사용하여 직접 실행해 볼 수 있다.
이 글에서도 위 링크 글과 마찬가지로 먼저 실수로 타원곡선의 특성을 이해한 후, 이를 모듈러 정수에서도 유사한 특성을 가지는 것을 확인하도록 한다. 그리고 이를 암호에 사용하는 방법을 정리해 본다.
실수 타원곡선
$a = -7, b=10$ 인 다음과 같은 타원 곡선을 이용하여 실수에서의 특징을 보자. 함수는 다음과 같은 모양이다.
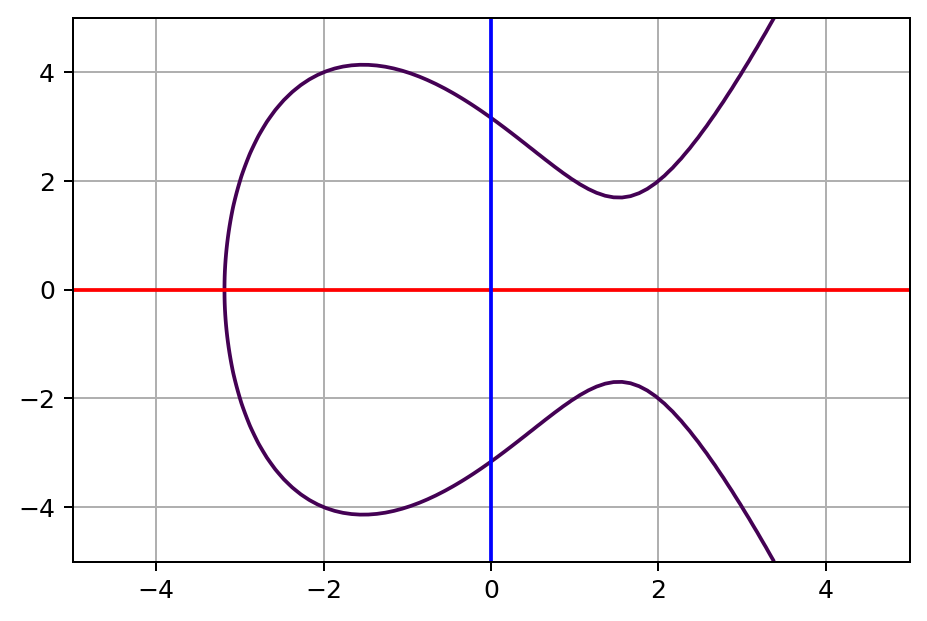
$y^2 = x^3 - 7x + 10$
타원곡선은 위 그림처럼 x축으로 대칭 형태를 가진다.
이 타원곡선의 임의의 두점을 지정하여 직선을 그어보면 다른 한점에 만나게 되는데, 이 교점이 흥미로운 특징을 가지고 있다.
우선 이를 확인하기 위하여 타원곡선의 임의 세점을 잡아보자.
- A: x=-1.0, y=4.0
- B: x=-2.0, y=4.0
- C: x=-0.1, y=3.2709325887275633
참고로 아래 그래프는 Fang-Pen의 Jupyter code를 이용하여 그린 것이다.
타원곡선의 임의의 두점을 직선으로 그어서 타원곡선과 만나는 점을 찾고 이의 x축으로 대칭인 점이 최종 결과라고 하자. 이렇게 찾는 과정을 우선 기호로 $\star$ 표시를 한다.
우선 A, B 점을 위와 같은 과정으로 결과 P를 구해본다.
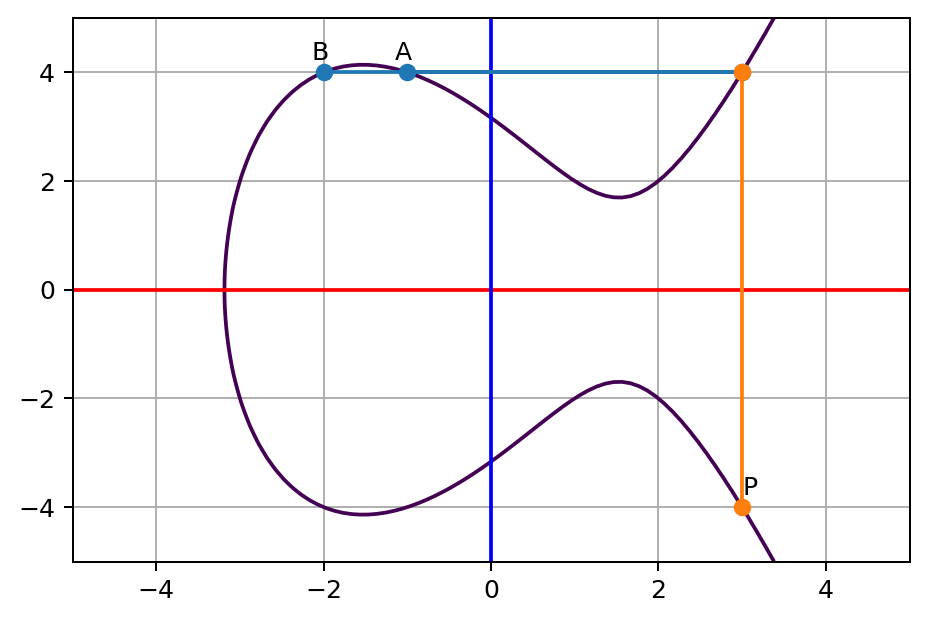
$A \star B = P$
이렇게 찾은 P 점을 다시 C 와 동일한 방식으로 다음 점을 찾아보면 다음과 같다.
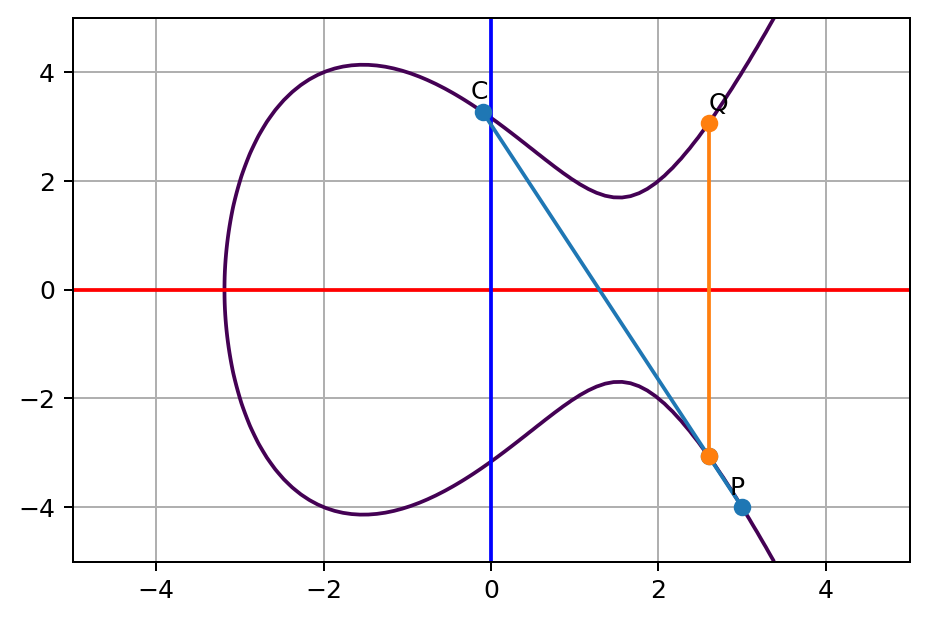
$P \star C = Q$
이번에는 동일한 연산을 순서를 바꾸어서 해본다. 우선 $B \star C = R$을 찾는다.
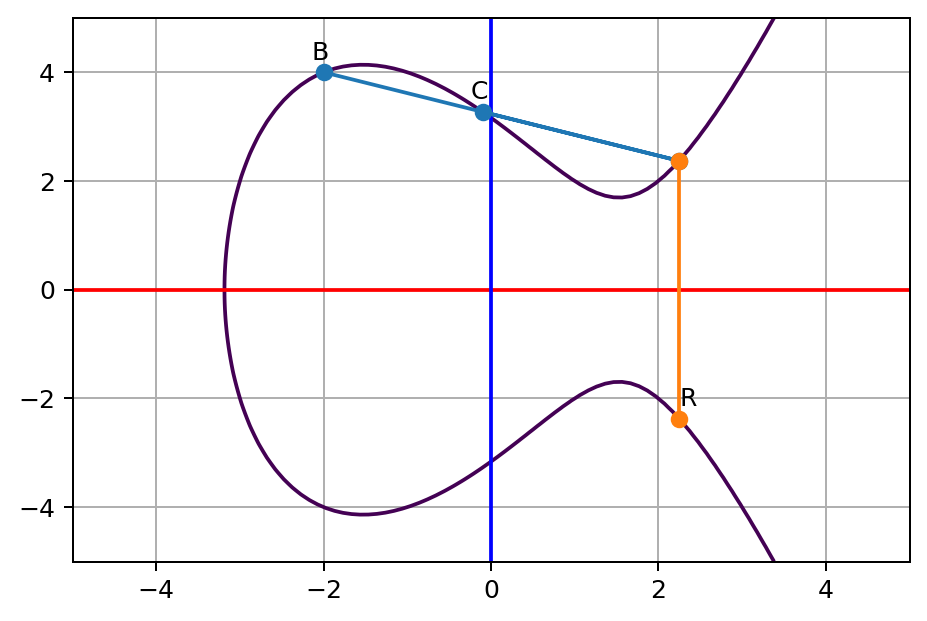
$B \star C = R$
이 R과 A로 동일한 방식으로 S를 찾는다.
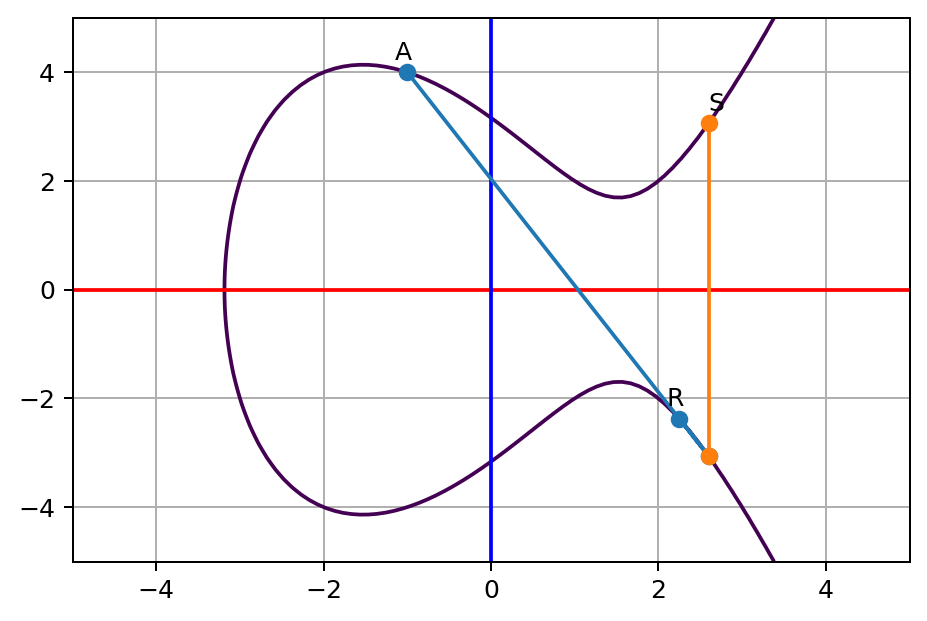
$A \star R = S$
위에서 구한 최종 결과값 Q와 S를 계산해보면 다음과 같다.
- Q: x=2.6011925816670645, y=3.0646123049731466
- S: x=2.601192581667065, y=3.0646123049731466
계산 결과를 보면 Python 실수의 정밀도 오류로 값이 약간 차이가 나는 것으로 실제로는 동일한 결과값을 가진다.
위 식을 다시 정리해 보면 다음과 같다.
$$(A \star B) \star C = A \star (B \star C)$$
그리고, 임의의 두점에서 다른 한점을 찾는 것이므로 다음과 같이 순서를 바꾸어 표현 할 수도 있다.
$$A \star B = B \star A$$
한가지 조건을 더 확인해 보자. 다음과 같은 A에 x축으로 대칭인 A’로 동일한 연산을 수행하면 어떻게 될까?
- A: x=-1.0, y=4.0
- A’: x=-1.0, y=-4.0
이 둘을 이은 선은 y축과 평행인 선으로 타원곡선과는 절대로 만나지 못한다. 이와 같은 무한 조건을 0 으로 표기해 보자. 그러면 다음과 같이 표시 할 수 있다.
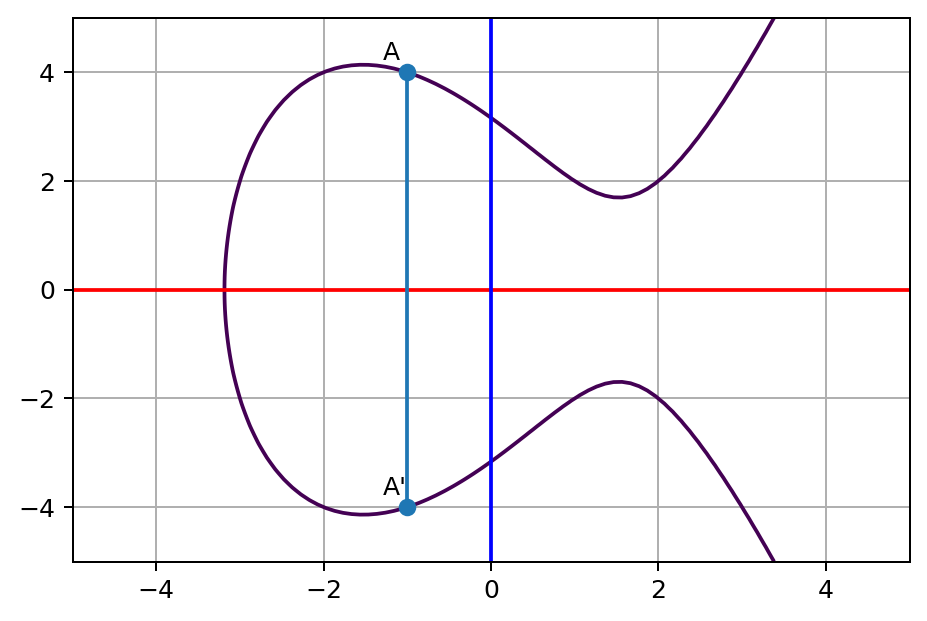
$A \star A’ = 0$
그리고 마지막, 같은 점과 같은 점에 대해서 연산은 어떻게 할까? 이때는 미분으로 접선을 구해서 다른 점을 찾을 수 있다.
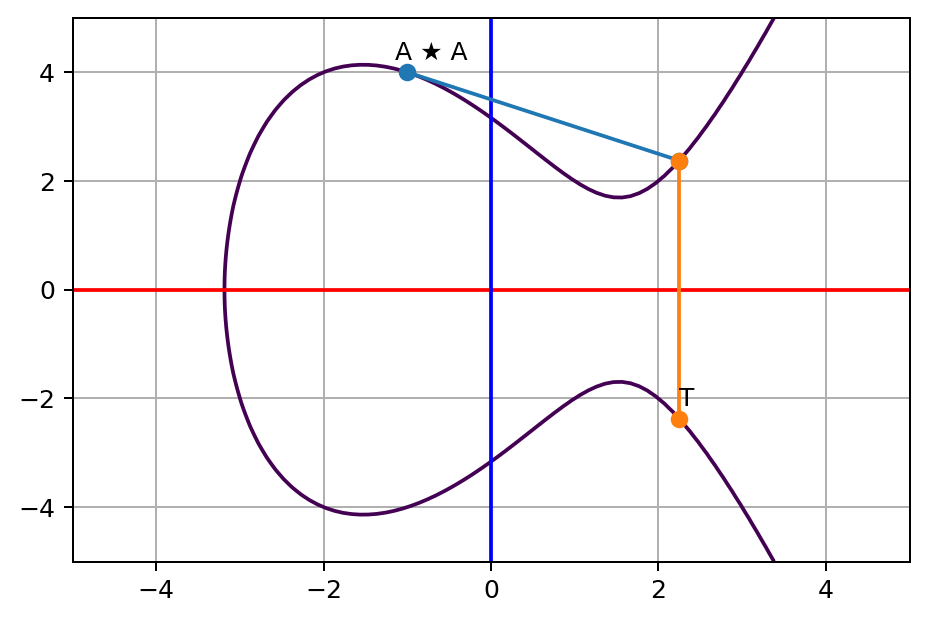
$A \star A = T$
지금까지 위의 $\star$ 연산을 보면 다음과 같다.
- 교환 법칙이 성립한다.
- $A \star B = B \star A$
- 결합 법칙도 성립한다.
- $A \star (B \star C) = (A \star B) \star C$
- 항등원이 존재하고, 역원도 존재한다.
- $A \star A’ = 0$
- $A \star 0 = A$
- 같은 수의 연산도 가능하고, 반복한 연산도 가능하다.
- $A \star A \star A \star A = A \star (A \star (A \star A)) $
위의 $\star$ 기호를 $+$ 로만 바꾸어 놓으면 일반 더하기 연산과 유사한 결과가 나오게 된다. 물론 연산과정이나, 항등원의 값은 다르지만 성질이 동일하다.
- 교환 법칙이 성립한다.
- $A + B = B + A$
- 결합 법칙도 성립한다.
- $A + (B + C) = (A + B) + C$
- 항등원이 존재하고, 역원도 존재한다.
- $A + A’ = 0$
- $A + 0 = A$
- 같은 수의 연산도 가능하고, 반복한 연산도 가능하다.
- $A + A + A + A = A + (A + (A + A)) = 4A $
같은 A를 반복하여 더한 결과는 곱하기와 같이 된다.
아래 tool로 직접 결과를 확인해 보수도 있다.
여기에서 n 값을 하나씩 증가하면서 결과 Q를 보면 타원곡선을 따라 무작위하게 이동하는 것처럼 보인다.
이 연산의 특징은 A를 수천번 더하는 일은 상당한 연산량이 필요하지만, 지수 연산과 비슷하게 곱하기로 연산량을 줄이는 것이 가능하다. 예를 들어 100번의 연산은 우선 A를 10번 더한 후 이 연산을 10번 더해보면 된다.
$ 100A = 10 (10A)$
실수 연산이 아니라, 유한체인 모듈로 정수 연산에서도 유사한 특성이 있다면 암호용도로 사용해볼 만 할 것이다.
타원곡선 실수 연산 식
타원 곡선의 연산은 그리 복잡하지는 않다.
우선 두 점 $P(x_p, y_p), Q(x_q, y_q)$을 이용하여 타원곡선과 만나는 점 $R(x_r, y_r)$는 다음과 같이 구할 수 있다.
- 다음 두 식에서 만나는 좌표를 계산
$$ \begin{align*} y^2 &= x^3 + ax + b \\ y &= mx + c \end{align*} $$
- c는 첫번째 점을 대입하여 다음과 같이 구함
$$ \begin{align*} y_p &= m x_p + c \\ c &= y_p - m x_p \end{align*} $$
- 처음 두식을 합쳐서 전개
$$ \begin{align*} (mx+c)^2 &= x^3+ax+b \\ m^2x^2+2mcx+c^2 &= x^3 + ax + b \\ x^3-m^2x^2 + (a-2mc)x + (b-c^2) &= 0 \end{align*} $$
- 위 수식은 세점을 이용한 $(x-x_p)(x-x_q)(x-x_r)=0$ 과 같은 형태이어야 한다.
$$ \begin{align*} (x-x_p)(x-x_q)(x-x_r)=0 \\ (x^2-(x_p+x_q)x+x_p x_q)(x-x_r)=0 \\ x^3-(x_p+x_q+x_r)x^2+(x_p x_q+x_q x_r+x_px_r)x-x_px_qx_r=0 \end{align*} $$
- $x^2$ 부분을 비교하면 다음과 같이 $x_r$를 구할 수 있다.
$$ \begin{align*} m^2 = x_p + x_q + x_r \\ x_r = m^2 - x_p - x_q \end{align*} $$
- 이 값을 1차 방정식에 대입하면 다음과 같다.
$$ \begin{align*} y_r &= m x_r + (y_p - mx_p) \\ &= m(x_r - x_p) + y_p \end{align*} $$
- $m$ 은 두 점 P, Q가 다른 경우 두 점의 기울기로 구하면 되고, 동일하면 미분으로 기울기를 구할 수 있다.
$$ s = \begin{cases} \frac{y_q-y_p}{x_q-x_p}, \quad P \neq Q (점의 덧셈) \\ \frac{3x_p^2+a}{2y_p}, \quad P = Q(점의 2배) \end{cases} $$
- 최종으로 구한 $y_r$를 반전 해주면 최종 결과 값을 구하게 된다.
Python코드의 Point 객체 연산도 동일한 방식으로 연산을 수행한다.
모듈러 정수연산에서의 타원 곡선
이제 암호 용도로 사용하기 위하여 유한체인 모듈로 정수연산으로 범위를 바꾸어 보자.
우선 임의의 소수 p 의 모듈러 연산을 수행하는 것을 보자.
$$ \begin{align*} x_r &= (m^2 - x_p - x_q) \mod p \\ y_r &= [y_p + m(x_r-x_p)] \mod p \\ &= [y_q + m(x_r - x_q)] \mod p \end{align*} $$
- $P \neq Q$ 이면,
- $m = (y_p - y_q)(x_p - x_q)^{-1} \mod p$
- $P = Q$ 이면,
- $m = (3x_p^2+a)(2y_p)^{-1}$
연산은 실수 연산과 거의 동일하다. 다만 차이가 있는 부분은 나누기 연산을 곱하기의 모듈러 역원으로 변경한 것이다.
이 곱하기 역원은 이산 대수 에서 정리한 ‘확장 유클리드 호제법’을 이용하여 계산할 수 있다.
다음은 $y^2=x^3-7x+10 \pmod p$ 에 대해서 $p$ 가 각각 19,97,127,487 인 경우의 결과를 점으로 찍어본 것이다. 가로축은 x 좌표이고, 세로축은 y 좌표 이다.
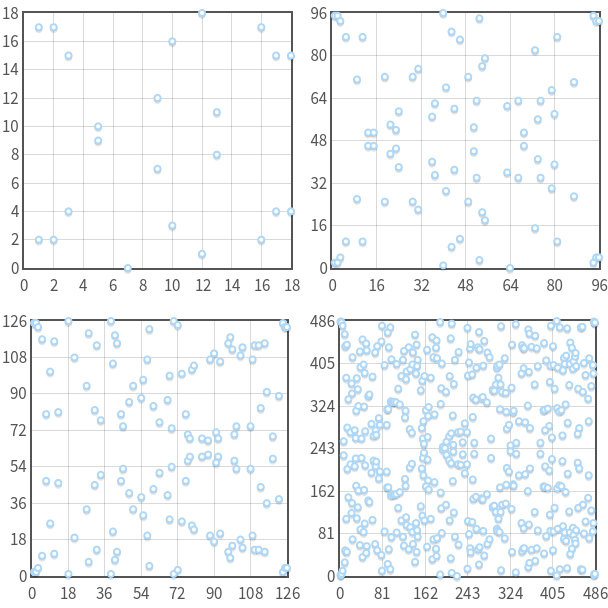
p=19, 97, 127, 487 인 경우
점의 모양이 타원곡선의 형태는 없지만, y축의 모듈러 중앙값을 기준으로 점이 대칭 형태로 구성되는 것은 동일하다.
임의의 큰 소수 p에 대해서 이와 같은 가능한 점들의 개수는 소수 p와 일치하지 않는다. 이 개수를 구하는 방법은 Schoof’s algorithm를 이용하여 구할 수 있다. 이와 같은 가능한 점의 개수를 Order of the group(N) 이라고 한다.
그런데 임의의 한 점을 골라서 같은 좌표를 계속 더하는 타원 곡선 연산을 수행해보면 실제로 모든 N 전체를 순환하지 않는다.
예를 들어 $y^2 \equiv x^3 + 2x+ 3 \pmod{97}$ 에서 $P=(3,6)$을 곱해보면 총 5개의 값만 순환하게 된다. 아래 링크에서 n 값을 증가시켜 보면 확인 가능하다.
Order of the group N은 100 개의 포인트 이지만, (80, 10), (80, 87), (3, 91), (Inf, Inf), (3, 6) 과 같이 총 5개의 포인트만을 순환한다(Inf는 실수 연산에서 말한 0점이다).
이와 같이 좌표 P를 Generator 또는 Base pointer 라고 하고, 이때의 이들 순환 그룹을 Cyclic subgroup(n) 라고 한다.
Cyclic subgroup(n)과 Order of the group(N)은 Lagrange’s theorem (group theory) 에 따라 다음과 같은 관계가 있다.
- N은 n으로 나누어 떨어짐. 즉, N의 약수 개수로 subgroup이 구성된다.
이제 암호화 용도로 사용할 조건이 어느정도 정리된 셈이다. 정리해 보면 다음과 같다.
- 모듈러 p 에 대해서 타원곡선 연산은 실수 연산과 동일하다.
- 단, p 에 대해서 가능한 점의 개수는 Order of the group(N) 개가 존재한다.
- 임의의 좌표에 대한 연산은 이 N 전체를 순환하지 않고, N의 약수 개수 만큼인 Cyclic subgroup(n)을 순환하다.
- 만일 이 n이 연산이 불가능하도록 큰 소수라면 암호화 용도로 적합하다.
연산이 이산 대수의 모듈러 지수 연산과 비슷하게 된다. 다만 이때는 지수 연산이지만, 타원곡선에서는 곱하기 연산 형태이다.
예를 들어 다음과 같은 조건을 생각해 보자.
- 모듈러 p와 generator P 포인트를 사전에 공개한다.
- Bob이 임의의 m을 선정하여 연산 값 $mP$를 Alice에게 전달한다.
- Alice도 임의의 n을 선정하여 연산 값 $nP$를 Bob에게 전달한다.
- Alice는 $n(mP)$로 최종값을 알수 있고, Bob도 $m(nP)$로 최종값을 알수 있다.
- 중간에 공격자는 p, P, mP, nP를 알지만 mnP를 실제적으로 구할 수 가 없다 (단순 무식하게 P를 모듈러 p에서 하나씩 더해 보는 수밖에 없다).
이렇게 하는 방식이 Diffie-Hellman의 ECC 버전이다.
문제는 적절한 Generator P와 Cyclic subgroup(n)을 찾아야 한다.
가장 단순하게 찾는 방법은 다음과 같다.
- Schoof’s algorithm를 이용하여 N을 계산
- N의 모든 약수를 찾음
- 모든 약수 n 에 대해서 nP를 계산
- 가장 작은 $nP=0$인 n을 찾으면 이 n이 subgroup n 이 된다.
실제로는 이 방식 보다는 적절한 n을 찾은 후 이를 만족하는 P를 선정하는 방식으로 찾는다.
이를 찾기 위하여는 우선 다음과 같은 조건을 알아야 한다.
- Lagrange’s theorem (group theory) 에 의해 $h=N/n$ 이런 정수 $h$ 가 있음. 이를 cofactor of the subgroup 이라고 함.
- 항상 모듈로 $NP = 0$ 임. 이를 다시 $h$로 풀어보면 $n(hP) = 0$ 이 됨.
- 보통 $n$은 소수를 사용하고, N의 약수임.
- $hP = G$ 를 계산
- 이 $G$ 가 0이 아니면 만족하는 n 이 됨. 만일 0 이면 subgroup은 order 1을 가짐.
- 이런 0이 아닌 P를 찾으면 됨
이와 같은 방식으로 P를 찾으면 암호화 모든 기본 값들을 구한 것이다.
마무리
내용이 길어지는 것 같아 우선 타원곡선의 더하기 연산의 특성에 대해서 실수, 모듈러 정수에서의 특징 및 원리를 설명하고 마무리 한다.
다음 글에서는 타원 곡선을 선정하는 방법과 이를 이용한 Diffie-Hellman의 키교환 방법과, DSA의 디지털 서명방법을 설명한다.