TLS/암호 알고리즘 쉽게 이해하기(12) - ECDH, ECDSA
이전 글 Elliptic Curve Cryptography(ECC)에서는 타원곡선 암호의 특징 및 알고리즘을 알아보았다.
이번에는 이를 활용한 암호화 응용과 실제 사용 예를 살펴보기로 한다.
ECC vs. RSA
공개키 암호화 방법으로 RSA와 비교하여 이야기 되나, 실제적으로 ECC는 RSA와 동일한 기능으로 사용하지는 않는다.
정확히는 RSA가 아니라 이산대수 문제를 이용한 DH 나 DSA 용도로 사용한다고 말할 수 있다.
RSA의 경우 아래와 같이 평문 $k$ 를 공개키 $e$로 모듈러 지수 연산을 하는 형식이다.
$$ E = k^e \pmod{n} $$
ECC의 경우 평문이 아닌 순환되는 subgroup 이 좋은 generator $G$를 선정하여 이를 키 $e$ 로 곱하는 것이다. $$ E = eG \pmod{p} $$
즉, 평문을 암호화 하는 용도로는 사용하지 않는다. 물론 RSA의 경우도 일반 평문을 암호화 하게 되면 분석적인 공격에 취약해질 가능성이 있으므로, hash 결과 값(서명 시)이나, 랜덤하게 만들어진 키 교환 등의 용도로만 사용을 권장한다.
ECDH 키교환
Diffie-Hellman Key Exchange 에서는 이산대수 문제인 모듈러 지수 연산의 어려움을 이용한 키교환 방법이었다.
이 지수 연산을 타원곡선의 곱하기 연산으로 대체한 것이 ECDH(Elliptic-curve Diffie–Hellman) 이다.
키교환 절차는 다음과 같다.
- Alice 와 Bob은 우선 domain prameter인 다음 값들을 교환한다. 이는 다른 사람들이 볼수도 있다.
- p: 모듈러 값
- G: Generator
- a, b: 타원 곡선의 a, b 값
- Alice는 자신의 비밀키 $d_a$ 를 선택하고, 공개키 $H_a = d_a G$ 를 계산하여 Bob에게 전달
- Bob도 자신의 비밀키 $d_b$ 를 선택하고, 공개키 $H_b = d_b G$ 를 계산하여 Alice에게 전달
- Alice와 Bob은 다음과 같이 키 S를 찾아냄
- $S = d_a H_b = d_a(d_b G) = d_b (d_a G) = d_b H_a$
- 공격자는 G, p, a, b를 알고, $H_a, H_b$ 를 얻는다고 해도 이를 풀수 있는 방법이 없다.
더하기 연산으로 표시되니까 오히려 DH 보다 이해하기가 편하다.
ECDSA
DSA에서 서명으로 힌트인 $r$ 값과 문서의 hash 값인 $x$가 포함된 $s$ 값을 서명값으로 사용하는 것이었다.
$$ \begin{align*} r &\equiv (\alpha^k \pmod p) \pmod q \\ s &\equiv \overline{k} (x + zr) \pmod q \end{align*} $$
ECDSA도 기본 골자는 비슷하다.
서명을 할 Alice는 domain parameter인 (G, p, a, b)를 정하고, 자신의 비밀키 $d_a$를 선택하고, 이를 이용하여 공개키 $H_a = d_a G$ 를 계산한다.
- 개인키는 $d_a$ 공개되지 않는다.
- Domain paramter (G, p, a, b) 와 공개키 $H_a$는 공개된다.
Alice 다음과 같이 서명한다.
- 1~$p$ 사이의 랜덤한 정수 $k$를 선택한다.
- $P = kG$를 계산한다.
- $P$ 값은 $(x_p, y_p)$ 포인트로 구성되는데 이 중 $x_p$를 이용하여 $r$을 계산한다.
- $r \equiv x_p \pmod {p}$
- 만일 $r=0$ 이면 다른 $k$를 선택하여 재계산 한다.
- 서명을 위한 hash 값은 $z$ 를 포함하여 다음 연산으로 $s$를 계산한다. 만일 hash 값 $z$가 $p$ 보다 크면 $p$의 비트 길이만 사용하고 상위는 버린다.
- $s \equiv \overline{k} (z + r d_a) \pmod {p}$
- 마찬가지로 $s=0$ 이면 다른 $k$를 선택하여 재계산 한다.
- $(r, s)$를 서명값으로 배포한다.
위 식에서 만일 subgroup order 가 소수가 아니면 위식을 사용할 수 없어, 키 선정 시 소수를 사용한다.
Bob 은 다음과 같이 검증한다.
- 다음 세 연산을 수행한다.
- $u_1 \equiv \overline{s}z \pmod p$
- $u_2 \equiv \overline{s}r \pmod p$
- $P = u_1 G + u_2 H_a$
- 위의 결과값 $P (x_p, y_p)$ 중 $r \equiv x_p \pmod {p}$ 이면 서명이 유효하다.
타원곡선의 종류
RSA, DH, DSA 와 같이 이산대수 문제를 이용하는 암호화 방법들은 초기 개인키를 생성하기 위하여 큰 소수를 찾는 과정이 필요하다.
마찬 가지로 타원곡선에서도 위에서 언급한 domain parameter 을 구하여야 한다. 이를 다시 정리해 보면 다음과 같다.
- p: 모듈러 값
- G: Generator
- a, b: 타원 곡선 $y^2=x^3+ax+b$ 의 a, b 값
- n: order of subgroup. G를 계속 더했을때 순환하는 그룹의 개수
- h: cofactor of subgroup.
앞에 보다 n, h 가 추가되었는데, 이는 이전 글 Elliptic Curve Cryptography(ECC)을 참조하면 된다.
어쨋든 이들을 계산하여야 하는데, 타원곡선에서는 이산대수와는 달리 사전에 정하여진 domain paramter를 사용한다.
다음과 같이 openssl 에서 지원하고 있는 타원곡선 종류를 확인 가능하다.
$ openssl ecparam -list_curves
secp112r1 : SECG/WTLS curve over a 112 bit prime field
secp112r2 : SECG curve over a 112 bit prime field
...
prime192v1: NIST/X9.62/SECG curve over a 192 bit prime field
prime192v2: X9.62 curve over a 192 bit prime field
...
sect113r1 : SECG curve over a 113 bit binary field
sect113r2 : SECG curve over a 113 bit binary field
...예를 들어 이 중 prime192v1 의 경우 domain parameter는 다음과 같은 값이다.
- p:
0xfffffffffffffffffffffffffffffffeffffffffffffffff - a:
0xfffffffffffffffffffffffffffffffefffffffffffffffc - b:
0x64210519e59c80e70fa7e9ab72243049feb8deecc146b9b1 - G: (
0x188da80eb03090f67cbf20eb43a18800f4ff0afd82ff1012,0x07192b95ffc8da78631011ed6b24cdd573f977a11e794811) - n:
0xffffffffffffffffffffffff99def836146bc9b1b4d22831 - h:
0x1
결국은 ECDH나 ECDSA를 사용하는 경우에는 이산대수 암호화 방법과는 달리 다음과 같은 절차를 거친다.
- 사용할 암호 강도 등을 고려하여 적절한 타원곡선을 선정 (예: prime192v1)
- 랜덤하게 자신의 비밀키를 선정
성능이 낮은 IoT 기기에서 RSA 2048 이나 RSA 3096 의 개인키를 생성하는 것은 성능에 따라서 수 분에서 수 십분이 소요될 수도 있는데, 타원곡선의 경우 랜덤으로 개인키를 생성만 하면 되기 때문에 이 부분도 하나의 큰 장점이 될 수 있다.
그렇다면 이들 타원곡선은 어떻게 선정되는 것일까?
인위적으로 특정 parameter로 만들어진 타원곡선은 취약점을 가지고 있다고 한다. 예를 들어 $p = hn$ 인 곡선은 Smart’s attack 으로 쉽게 풀릴수 있다고 한다. 의도적으로 이런 취약점을 가진 곡선을 만드는 것을 막는 방법 중 하나로 타원 곡선의 parameter a,b 선정 시 다음과 같은 방법을 이용하기도 한다.
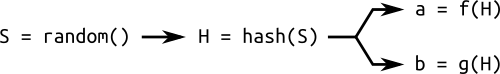
Paramter a, b 결정방법
이와 같이 random seed를 hash 함수를 이용하여 최종적으로 만들어진 a, b를 사용하도록 한다면 이와 같은 의도성을 막을 수 있다. 보통 이 hash 함수로 SHA-1 을 사용한다.
이제 각 타원곡선이 어떻게 만들어 졌는지 찾아보자. 아래 링크를 보면 사용하고 있는 모든 타원곡선에 대해서 정보를 얻을 수 있다.
예를 들어 prime192v1는 다음과 같이 정보를 얻을 수 있다.
- ANSI X9.62 표준으로 정의된 prime192v1 의 정보는 아래 링크에 있다.
- 상단에는 위 domain paramter 값들을 확인할 수 있고, 그 아래에 Seed 값이 명기되어 있다. 이 Seed 값을 이용하여 a, b 가 선정된 것이다.
- Seed:
3045AE6FC8422F64ED579528D38120EAE12196D5
- Seed:
- Seed 값으로 SHA-1 hash로 a, b를 구하는 방법은 아래 링크에서 확인할 수 있다.
타원곡선에 따라서 domain parameters를 선정하는 방식은 다르지만, 사용 방법은 지정된 domain parameter를 이용하여 동일하다.
타원곡선 선정
Standard curve database 보면 종류가 많은데, 이중 어느 것을 사용할지 고민이 될 수 있다.
일단 NIST Recommendatations (2020)을 참고하면 160bit 이하의 타원곡선은 사용하여서는 안된다. 다음과 같은 곡선들이 이에 해당한다.
- secp112r1, secp112r2, secp128r1, secp128r2, secp160k1, secp160r1, secp160r2, secp192k1
2018년 글이기는 하나 아래 링크를 참고할 만도 한다.
이를 보면 다음 순으로 많이 사용한다고 한다.
- P-256 (secp256r1, prime256v1)
- X25519
- P-512 (secp512r1)
- P-384 (secp384r1)
256bit인 P-256 을 현 시점에서 가장 많이 사용한다.
Block Cipher의 ‘암호화 키 길이’에 정리한 것과 같이 P-256이면 AES 128, RSA-3072와 유사한 암호화 강도를 가진 것이다. 이를 다시 정리해 보면 다음과 같다.
| 계열 | 암호시스템 | 80bit | 128bit | 192bit | 256bit |
|---|---|---|---|---|---|
| 인수분해 | RSA | 1024 | 3072 | 7680 | 15360 |
| 이산대수 | DHKE, DSA, Elgamal | 1024 | 3072 | 7680 | 15360 |
| 타원곡선 | ECDH, ECDSA | 160 | 256 | 384 | 512 |
| 대칭암호 | AES | 80 | 128 | 192 | 256 |
P-256, secp256r1, prime256v1 은 모두 동일한 것을 말하는 것으로 표준을 정리한 곳에 따라서 이름이 다르다. 관련 테이블은 아래 링크를 참고 할 수 있다.
| SECG | ANSI X9.62 | NIST |
|---|---|---|
| secp192r1 | prime192v1 | NIST P-192 |
| secp224r1 | NIST P-224 | |
| secp256r1 | prime256v1 | NIST P-256 |
| secp384r1 | NIST P-384 | |
| secp521r1 | NIST P-521 |
X25519 는 Curve25519 타원함수를 사용하는 것으로 ECDH는 X25519, ECDSA는 ED25519 라고 한다.
P-256은 NIST 에서 정의한 것이라 많이 사용하는 이유는 명확한데, X25519를 많이 사용하는 이유는 다음과 같다고 한다.
- 설계자인 Daniel J. Bernstein (DJB)가 소스 및 관련 자료를 아래 링크에 공개하였고, 특허도 없고, timing attack에도 안전하도록 설계하였다.
- IETF TLS 1.3에 X25519, ED25519가 추가되었고, NIST에서도 2017년에 Special Publication SP 800-186 에 추가되어서, 미정부에서 사용도 승인되었다.
- P-256에 비교하여 40% 정도 연산량이 적어, 특히 저사양 CPU를 사용하는 IoT 기기에 좋다.
- 많은 브라우저나 TLS 업체에서 지원한다.
OpenSSL command line에서는 아직은 Curve25519를 지원하지 않아 genpkey 명령으로 직접 만들어서 사용하여야 한다.
이상으로 정리해 보면 다음과 같이 사용하면 될 것 같다.
- 일반적인 용도라면 P-256 사용
- 보안 강도를 높일 필요가 있다면 P-512 사용
- IoT 기기 등 저사양을 고려한다면 X25519, ED25519 사용
IoT 기기에서 사용하여 X25519, ED25519를 사용한다면 libsodium 등의 library를 사용할 수 있다.
Openssl 로 동작 확인
ECDH 시험
Openssl을 이용하여 ECDH를 확인 해본다.
- 우선 지원되는 curve를 확인한다.
$ openssl ecparam -list_curves- ecparam subcommand로 Alice의 개인키를 생성한다. 여기에서는 P-256 (prime256v1)을 생성하였다.
$ openssl ecparam -name prime256v1 -genkey -noout -out alice-priv.pem- 생성된 개인키는 다음과 같이 확인 가능하다.
- Private key는 랜덤하게 생성된 것으로 이 경우 256bit의 길이가 맞다.
- Public key의 경우 private 보다 약 2배 가량 되는데, 이유는 위에서 처럼 $H_a = d_a G$ 와 같이 x,y 좌표를 가진 Genearator G와 곱한 결과인 x, y 좌표와 1bit의 parity 가 추가되었기 때문이다.
$ openssl ec -in alice-priv.pem -text -noout
read EC key
Private-Key: (256 bit)
priv:
1c:6d:99:e3:18:fa:78:0e:9e:08:a7:81:95:49:0c:
e5:b3:6e:26:7b:40:76:94:c3:79:74:50:98:cd:db:
f4:bf
pub:
04:c0:00:72:22:80:b6:27:12:78:4e:a2:9c:1f:6b:
3c:e5:96:b2:24:94:59:3c:a0:5f:64:36:ef:f4:1b:
32:34:38:e1:cf:84:9a:ed:08:27:30:ee:6c:08:13:
32:c5:0c:96:fc:1a:99:97:f2:d5:5c:5f:bc:fd:b9:
ed:f5:6d:a9:8e
ASN1 OID: prime256v1
NIST CURVE: P-256- 개인키로 공개키를 생성한다.
$ openssl ec -in alice-priv.pem -pubout -out alice-pub.pem- 동일한 방식으로 Bob의 개인키와 공개키를 생성한다.
$ openssl ecparam -name prime256v1 -genkey -noout -out bob-priv.pem
$ openssl ec -in bob-priv.pem -pubout -out bob-pub.pemAlice와 Bob은 prime256v1 타원곡선 정보와 각자 자신의 공개키를 상대방에게 전달하였다고 하자.
Alice는 Bob의 공개키를 이용하여 키를 유도할 수 있다.
$ openssl pkeyutl -derive -out alicebob.key -inkey alice-priv.pem -peerkey bob-pub.pem- Bob도 Alice의 공개키를 이용하여 키를 유도할 수 있다.
$ openssl pkeyutl -derive -out bobalice.key -inkey bob-priv.pem -peerkey alice-pub.pem- 둘이 생성한 키 값을 비교하면 아래와 같이 동일한 것을 알수 있다.
$ hexdump alicebob.key
0000000 f5d1 d9f7 cb35 be15 51af d264 b90f 4bb7
0000010 c031 dae3 ed42 71c4 f3b1 c0a5 42f1 7955
$ hexdump bobalice.key
0000000 f5d1 d9f7 cb35 be15 51af d264 b90f 4bb7
0000010 c031 dae3 ed42 71c4 f3b1 c0a5 42f1 7955ECDSA 시험
위에서 생성한 Alice의 키를 이용하여 서명을 해본다.
- 서명할 파일 생성
$ echo 1234567890 > mydata.txt- dgst subcommand로 SHA-256 해시함수를 사용하여 서명한다.
$ openssl dgst -sha256 -sign alice-priv.pem -out mydata.sha256 mydata.txt- 서명파일은 DER 인코딩 된 것으로 asn1parse 로 확인하면 다음과 같이 256bit의 두 값 r 과 s가 차례대로 들어 있는 것을 확인할 수 있다.
$ openssl asn1parse -in mydata.sha256 -inform DER
0:d=0 hl=2 l= 68 cons: SEQUENCE
2:d=1 hl=2 l= 32 prim: INTEGER :56E84F9DC7396284C9E03B78DF1AE024E5EE86051EAC52AB02B940A861A5C62F
36:d=1 hl=2 l= 32 prim: INTEGER :78831E8F60EE73AD23DFB43E5A460A5ADB4A75C49CA5AAEA49ACEE37D94C5C36- 서명 검증은 alice의 공개키를 이용하여 할 수 있다.
$ openssl dgst -sha256 -verify alice-pub.pem -signature mydata.sha256 mydata.txt
Verified OK마치며
지금까지 정리한 사항으로 대칭키, 비대칭키 암호, 해시, 키 합의, 서명 등 암호화의 기본이 기능이 정리된 것 같다.
다음에는 이들을 조합하여 인증 방식 및 TLS 표준을 정리할 예정이다.