TLS/암호 알고리즘 쉽게 이해하기(9) - Digital Signature
DSA는 Digital Signature Algorothm 의 약자로, 미국 NIST 에서 제정한 디지털 서명 알고리즘이다.
이번 글에서는 이와 같은 디지털 서명에 관한 전반적인 사항을 다음과 같은 순서로 정리한다.
- RSA 서명 알고리즘
- ElGamal 서명 알고리즘
- DSA 서명 알고리즘
- OpenSSL 을 이용한 동작 확인
RSA Signature
RSA 서명 방식은 앞의 RSA 글에서 언급한 것과 같이 개인키로 문서의 Hash 값을 암호화 하는 것으로 RSA의 동작 원리를 알고 있으면 직관적이다. 관련 표준은 PKCS#1의 8장 을 보면 된다.
서명 절차는 아래와 같다.
- Alice는 사전에 자신의 공개키를 배포한다.
- 문서를 아래와 같이 SHA-1 과 같은 hash 함수를 이용하여 줄이고, 이를 RSA 암호 블럭 크기에 맞추어 적절히 패딩을 추가
- 이를 자신의 RSA 개인키로 암호화 (서명)
- 문서와 서명을 같이 배포
graph LR; subgraph RSA 서명 A1([문서]) --> B1[Hash] --> B2([Hash값+Padding]) --> C1[RSA 개인키 암호] --> D1([서명]) end style B1 fill:#FFF9C4 style C1 fill:#FFF9C4
문서와 서명을 받은 Bob은 다음과 같은 절차로 검증을 할 수 있다.
- 서명 데이타를 Alice의 공개키로 복호화
- 패딩 값들이 적절한지 확인
- 본문의 Hash 결과와 위 복호화 한 결과가 일치하는지 확인
graph LR; subgraph RSA 서명 D1([서명]) --> C1[RSA 공개키 복호] --> B1[Hash값 + padding] end style C1 fill:#FFF9C4
RSA 의 개인키가 없으면 이와 같은 암호화(서명)를 할 수 없다는 것을 이용하는 방식이다.
RSA 에서 언급하였던 것과 같이 보통 RSA 공개키 값은 65537(0x10001) 과 같이 개인키에 비하여 상대적으로 짧은 값이다. 이는 더 자주 사용하는 검증을 위한 연산량이 서명을 위한 연산량보다 작다는 장점도 있다.
ElGamal Signature
ElGamal Algorithm은 RSA 처럼 이산대수 문제를 이용하는 방식이다.
ElGamal 방식도 RSA 처럼 암호화와 서명 두 가지 방식을 지원한다. RSA의 경우 암호화나 서명이나 어떤 데이타를 어떤 키로 암호화 하는지만 다르지만, ElGamal 방식은 암호화와 서명 방법이 조금 다르다.
우선은 이를 이해하기 위하여 이산대수 문제를 간략히 다시 정리해 본다.
소수 모듈러 연산은 사칙연산에 닫혀 있고, 교환법칙, 결합법칙도 성립한다.
페르마의 소정리에 의하여 소수 $p$ 보다 작고 0보다 큰 양수 $k$ 에 대해 다음 식이 항상 성립한다.
- $k^{p-1} \equiv 1 \pmod p$
아래 처럼 양변에 $k$ 를 곱해서 지수만 보면 $(p-1)$의 모듈러 연산이 된다.
- $k^p \equiv k^1 \pmod p$
- $p = 1 \pmod {p-1}$
$(p-1)$ 과 서로소인 $s$ 를 임의로 선정하면, 확장 유클리드 호제법으로 모듈러 $(p-1)$ 에서 $s$의 곱하기 역원 $t$를 찾을 수 있다.
위에서 찾은 $p$, $s$, $t$ 가 이산대수 암호화의 기본적인 요소로 사용된다. 조금 더 자세한 내용은 이산대수 문제 를 참고하면 된다.
ElGamal Encryption
Bob은 다음과 같이 키를 만든다.
- 큰 소수 $p$ 선정
- $p$ 보다 작은 임의의 숫자 primitive root $\alpha$, 비밀키 $z$를 선정하여 다음과 같이 $\beta$ 를 계산
- $\beta \equiv \alpha^z \pmod p$
- $(p, \alpha, \beta)$는 공개키, $z$은 개인키로 공개키를 사전에 공유한다.
Alice는 Bob의 공개키를 이용하여 평문 $m$을 다음과 같이 암호화 한다.
- $(p-1)$ 과 서로소인 임의의 랜덤 $k$를 선택
- 다음과 같은 $r, s$를 계산
- $r \equiv \alpha^k \pmod p$
- $s \equiv m \beta^k \pmod p$
- $r, s$를 전송 ($k$는 비공개)
$s$는 평문이 $\beta^k$가 곱해져 암호화된 값이고, $r$은 이를 풀기 위한 힌트라고 볼 수 있다.
Bob은 $\beta^k$의 모듈러 $p$에 대한 곱하기 역원만 구하면 된다. Bob은 다음과 같이 연산을 하여 복호화 할 수 있다.
- $s$ 에 포함된
$\beta^k \pmod p$ 는 다음과 같이 변형하여 $r$ 로 부터 얻을 수 있다.
- $\beta^k \equiv (\alpha^z)^k \equiv (\alpha^k)^z \equiv r^z \pmod p$
- 위의 값을 얻은 후 이를 확장 유클리드 호제법을 이용하여 모듈러 곱하기 역원 $\overline{\beta^k}$ 를 계산한다.
- 이를 $s$에 곱하여 원문을 얻는다.
- $s \overline{\beta^k} \equiv (m \beta^k) \overline{\beta^k} \equiv m \pmod p$
암호화를 하면 데이타량이 두배가 되지만, 동일한 원문을 동일한 키로 암호화를 하는 경우에도 랜덤 $k$ 로 인하여 암호화 결과가 매번 달라지는 장점이 있다.
다른 모든 암호 알고리즘과 마찬가지로 이 random $k$ 값을 재사용하면 암호가 쉽게 깨지는 문제가 있어 주의하여야 한다.
ElGamal Signature
서명도 암호화와 비슷하지만 약간 다르게 적용된다.
서명을 할 Alice는 암호화 방식과 동일하게 다음과 같은 키를 만든다.
- 큰 소수 $p$ 선정
- $p$ 보다 작은 임의의 숫자 primitive root $\alpha$, 비밀키 $z$를 선정하여 다음과 같이 $\beta$ 를 계산
- $\beta \equiv \alpha^z \pmod p$
- $(p, \alpha, \beta)$는 공개키, $z$은 개인키로 공개키를 사전에 공유한다.
Alice는 자신의 개인키로 원문 $m$을 다음과 같이 서명한다.
- $(p-1)$ 과 서로소인 임의의 랜덤 $k$를 선택
- 다음과 같은 $r, s$를 계산. $\overline{k}$는 $k$의 모듈러 $(p-1)$의 곱하기 역원이다.
- $r \equiv \alpha^k \pmod p$
- $s \equiv \overline{k} (m - zr) \pmod {p-1}$
- 원문 $m$과 서명 $(r, s)$를 전송
Bob은 다음과 같이 두 연산을 수행하여 비교한다.
- $v_1 \equiv \beta^r r^s \pmod p$
- $v_2 \equiv \alpha^m \pmod p$
- 위 두 값 $v_1 \equiv v_2$ 이면 검증 OK
알고리즘의 검증은 조금 복잡한데 다음과 같이 확인할 수 있다.
- 우선 $s$에 $k$를 곱하여 제거한다.
- $sk \equiv \overline{k} (m - zr)k \equiv (m-zr) \pmod {p-1}$
- 이를 $m$ 으로 다시 정리해 보면 다음과 같다.
- $m \equiv sk + zr \pmod {p-1}$
- 위 $v_2$의 $m$을 위의 값으로 치환하면 다음과 같다.
- $v_2 \equiv \alpha^m \equiv \alpha^{sk+zr} \equiv \alpha^{sk} \cdot \alpha^{zr} \equiv (\alpha^k)^s \cdot (\alpha^z)^r \equiv r^s\beta^r \equiv v_1 \pmod p$
위와 같이 지수 $m$을 $sk + zr \pmod {p-1}$ 로 대체할 수 있는 것은 페르마 소정리에 의하여 지수만 보면 $(p-1)$ 모듈러 연산 형태가 되기 때문이다.
ElGamal 활용
TLS에서 ElGamal 방식은 직접적으로는 사용하지 않는다.
지금은 RSA도 특허가 만료되어 큰 장점은 아니지만 초기에 ElGamal 방식은 특허가 없어서 오픈소스 암호화 알고리즘에서 많이 사용하였다. PGP(Pretty Good Privacy) 도 이를 기반으로 공개키를 사용한다.
ElGamal 서명은 직접적으로 사용하지는 않으나 상용을 포함한 많은 서명 알고리즘이 이를 기반으로 하고 있다. 다음에 설명할 DSA, ECDSA가 이를 기반으로 하는 서명 알고리즘이다.
DSA Signature
DSA를 이해하기 위하여는 ElGamal 서명을 먼저 알고, 이와 어떻게 다른지를 이해하는 것이 좋다.
DSA는 ElGamal의 취약점을 개선한 것으로 다음과 같은 장점이 있다.
- ElGamal에 비하여 연산이 빠르다.
- DSA는 두개의 서로 다른 이산대수 공격을 공격을 하여야만 풀 수 있다.
- 서명 크기가 작다.
서명은 다음과 같은 절차로 수행한다.
서명을 할 Alice는 다음과 같은 방식으로 키를 만든다.
- 두 소수 $p$ 와 $q$를 찾는다.
- $p$는 1024bit 길이의 임의의 소수를 선정한다.
- $q$는 160bit 길이의 소수이면서, $(p-1)$ 의 약수인 임의의 수를 선정한다. (1024bit, 160bit는 임의로 정한 길이로 암호화 강도에 따라 조정이 된다)
- 소인수 분해가 어려우므로 실제로는 $q$를 먼저 선정하고, 이에 맞는 $p$를 찾는다.
- Primitive root $g$를 임의로 선정하여 다음과 같이 $\alpha$를 계산한다.
- $\alpha \equiv g^{(p-1)/q} \pmod p$
- 위 수식의 의미는 페르마 소정리($g^{p-1}\equiv 1 \pmod p$)에 의하여 다음과 같은 의미가 된다.
- $\alpha ^q \equiv 1 \pmod p$
- 비밀키 $z$ 를 선정하여 다음과 같이 $\beta$ 를 구한다.
- $\beta \equiv \alpha ^ z \pmod p$
- 위에서 얻은 $(p, q, \alpha, \beta)$ 는 공개키가 되고, $z$ 은 비밀키가 된다.
- 위 식을 보면 전체는 모듈러 $p$ 연산이지만, 지수부는 모듈러 $q$ 연산이 된다.
DSA에서는 서명 시 본문을 그대로 사용하지 않고, SHA 같은 hash 함수를 이용한 축약된 hash 값을 서명한다($q$ 값은 이 hash 크기 보다는 큰 수가 되어야 한다).
Alice는 다음과 같이 서명한다.
- $(q-1)$보다 작은 임의의 랜덤값 $k$를 선정한다.
- 본문 $m$의 hash 값 $x$를 얻는다.
- 다음과 같이 $r, s$ 를 구한다. ($r$은 $p, q$ 각각의 모듈로 연산을 함)
- $r \equiv (\alpha^k \pmod p) \pmod q$
- $s \equiv \overline{k} (x + zr) \pmod q$
- 서명으로 $x, (r,s)$를 본문 $m$과 같이 전달한다.
Bob은 다음과 같이 서명을 검증한다.
- 다음 세 연산 수행
- $u_1 \equiv \overline{s}x \pmod q$
- $u_2 \equiv \overline{s}r \pmod q$
- $v \equiv (\alpha^{u_1} \beta^{u_2} \mod p) \pmod q$
- $v = r$ 이면 검증 OK
검증은 다음과 같이 할 수 있다.
- 우선 $s$에 $k$를 곱하여 $\overline{k}$를 제거한다.
- $ks \equiv x + zr \pmod q$
- 이를 다시 $s$의 역원 $\overline{s}$를 곱하여 $s$를 제거한다.
- $k \equiv ks\overline{s} \equiv x \overline{s} + zr \overline{s} \pmod q$
- 이식을 위에서 구한 $u_1$ 과 $u_2$로 치환한다.
- $k \equiv u_1 + z u_2 \pmod q$
- $r$ 식의 지수부는 $q$의 모듈러 연산이므로, 위의 $k$로 치환 할 수 있다. $$ \begin{align*} r &\equiv (a^k \bmod p) \bmod q \\ &\equiv (\alpha^{u_1 + zu_2} \bmod p) \bmod q \\ &\equiv (\alpha^{u_1} (\alpha^z)^{u_2} \bmod p) \bmod q \\ &\equiv (\alpha^{u_1}\beta^{u_2} \bmod p) \bmod q \end{align*} $$
- 결과로 $r \equiv v$ 가 된다.
DSA는 암호화에 사용시 키 길이에 따라 다음과 같은 $p$ 와 $q$ 를 사용한다. 이때의 서명 길이는 $r,s$ 로 $q$ 길이의 2배가 된다.
| p | q | 서명길이 | 노트 |
|---|---|---|---|
| 1024 | 160 | 320 | 보안상 더이상 사용치 않음 |
| 2048 | 256 | 512 | 초기에는 q로 224bit를 사용하나, 지금은 256bit를 이용 |
| 3072 | 256 | 512 |
OpenSSL
위의 알고리즘을 OpenSSL 을 이용하여 확인을 해보자.
RSA Signature
우선 다음과 같이 RSA private, public key를 생성한다. 키 생성에 대한 설명은 이전 글 RSA를 참조하면 된다.
| |
서명할 임의의 데이터를 생성한다.
| |
openssl dgst 명령을 이용하여 다음과 같이 서명을 하면 서명파일 sha1.sign 이 생성된다.
- Message Digest Algorithm: SHA-1
- Padding Scheme: PKCS#1 v1.5
| |
서명 검증은 다음과 같이 한다.
| |
서명 전의 원문 파일은 PKCS#1 v1.5 padding 형식으로 다음과 같은 구조를 가진다.
- PKCS#1v1.5 padding scheme 구성: 00||01||PS||00||T||H
- H: SHA-1 으로 계산된 hash 값
- T: ASN.1 로 encoding된 SAH-1 magic bytes
- PS: 암호 블럭의 나머지 공간을 0xff 로 패딩. RSA-2048 의 경우 256-38=218바이트
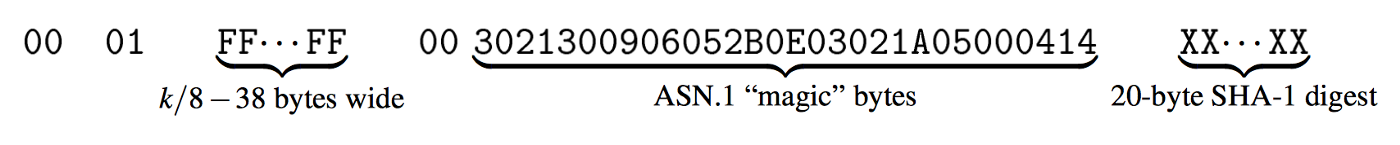
PKCS#1 v1.5 padding
이번에는 openssl rsautl 을 이용하여 풀어보자.
| |
-verify 명령은 실제로 검증까지는 하지 않고, 공개키로 복호화하여 padding을 제거한 데이타를 출력한다.
sha1의 결과값이 뒤에 들어가 있는 것을 확인할 수 있다.
앞에 들어간 3021300906052b0e03021a05000414 magic byte는 ASN.1 이라는 형식으로 인코딩 된 것으로 -asn1parse 옵션을 추가하여 확인할 수 있다.
| |
DSA Signature
우선 다음과 같이 2048bit DSA 개인키와 공개키를 만든다.
| |
dsa_priv.pem 의 내용을 보면 다음과 같이 구성된다.
| |
위의 설명과 비교하면 다음과 같이 된다.
- $z$; priv
- $p$: P
- $q$: Q
- $\alpha$: G
- $\beta$: pub
서명은 다음과 같이하여 생성할 수 있다.
| |
Q가 256bit(32bytes)로 서명은 2배 길이인 64bytes이어야 하는데, 파일 크기가 70bytes 인 것은 서명이 ASN.1 DER encoding 되어 있기 때문이다.
다음과 같이 256bit의 $r$ 과 $s$ 를 확인할 수 있다.
| |
서명 검증은 다음과 같이 할 수 있다.
| |
마치며
서명과 관련된 사항을 전반적으로 정리 하다보니 내용이 길어진 것 같다. 이산대수로 정리한 부분만 제대로 이해하면 ElGamal 이나 DSA 알고리즘에 대해서는 이해할 수 있을 것이다.
서명과 관련된 표준은 미국 NIST 에서 정의한 FIPS 186-4, Digital Signature Standard (DSS) 를 참고할 수 있다. 이 문서에는 DSA, RSA 서명, ECDSA 에 대해서 정의되어 있다.
ECDSA는 DSA 의 이산대수 문제를 Elliptic Curve (EC) 로 대체하는 알고리즘으로 다음 기회에 타원곡선 알고리즘에서 설명할 예정이다.